Table of Contents
- Intorduction
- What is LZ4?
- How Does LZ4 Work?
- Best-Suited Data Types for LZ4
- Data Types Less Suitable for LZ4
- Optimization Tips for Using LZ4 in Columnar Databases
- Conclusion
Intorduction
Data compression has become a cornerstone of efficient storage and faster data transfers. Among the myriad of compression algorithms available, LZ4 stands out for its speed. It achieves remarkable compression and decompression speeds while maintaining reasonable compression ratios. This blog explores the inner workings of LZ4, its practical use cases, and its advantages over other algorithms.
What is LZ4?
LZ4 is a lossless compression algorithm based on the LZ77 algorithm. It compresses data by identifying repeating patterns and encoding them in a compact format. The focus of LZ4 is on high-speed compression and decompression, making it suitable for real-time applications where performance is critical.
It's also default compression algorithm for most Columnar DB like Clickhouse
Key Features of LZ4
High Speed:Compression and decompression speeds of 400-500 MB/s per core. Ideal for scenarios where speed is more critical than compression ratio.Small Memory Footprint:LZ4 works with Sliding window approach reduces memory usage compared to dictionary-based algorithms.Streaming-Friendly:Supports block-based compression, making it suitable for streaming large data sets.
How Does LZ4 Work?
LZ4 is based on the principles of the LZ77 algorithm. Put simply, it identifies repeating patterns in the data and replaces them with a reference to where they previously occurred. This reference is stored as an offset-length pair, which points to the location and size of the repeated sequence. Instead of storing duplicate data, LZ4 efficiently compresses it by specifying the position (offset) and how many bytes (length) to reuse from the previously processed data.
Now we will discuss in detail, how exactly it does that
The Building Blocks
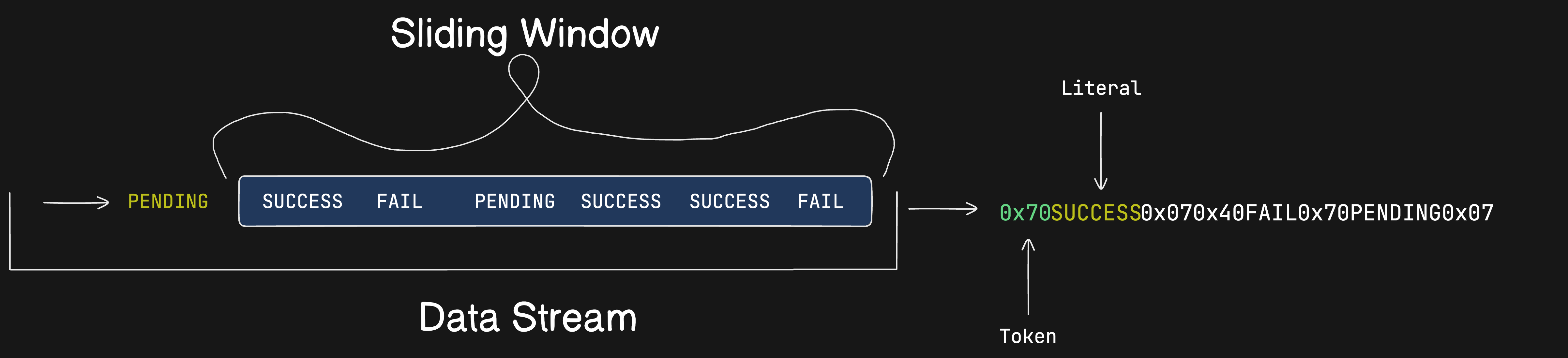
Sliding Window(Dictionary)
LZ4 maintains a sliding window (default: 64 KB) to store the recently processed data.
This window acts as a "dictionary" to find repeating patterns.
It is not stored in the compressed file. It is transient and exists only in memory during compression and decompression
During compression:Used to find matches in the input data.During decompression:Reconstructed incrementally by copying previously decompressed data into the output buffer.Tokens
The compressed data is represented as tokens, it is a single byte (8 bits) that serves as a compact descriptor for a segment of compressed data. It encodes two key pieces of information:
Literals:Uncompressed raw data.Matches:(offset, length) pairs pointing to previous sequences.
| Literal Length (4 bits) | Match Length (4 bits) |
The first 4 bits represent the length of the literal. The next 4 bits represent the length of the match, minus 4 (because matches shorter than 4 bytes are not encoded).
If the literal length or match length exceeds 15 (the maximum that can fit in 4 bits), additional bytes are used to encode the length.
"SUCCESS"
TOKEN: 0x70 (If encountered fist time)
TOKEN: 0x07 (If encountered again within sliding window)
Calculation of token, for above Example:
| Property | First Occurrence | Matched Occurrence |
|---|---|---|
| Literal | SUCCESS (7 bytes) | No new literal |
| Literal Length (4 bits) | 7 (binary: 0111) | 0 (binary: 0000) |
| Match Length (4 bits) | 0 (binary: 0000) | 7 (binary: 0111) |
| Binary Representation | 0111 0000 | 0000 0111 |
| Hex Representation | 0x70 | 0x07 |
Hash Table
The hash map (or hash table) is a runtime data structure that facilitates fast pattern matching for compression. It is a fixed-size array that stores positions of 4-byte sequences (substrings) in the sliding window. It allows the compressor to quickly look up previously encountered sequences to find repeating patterns
Size of HashMap is proportional to the sliding window size (default: 64 KB → 65536 entries).
How Hash Table is populated:
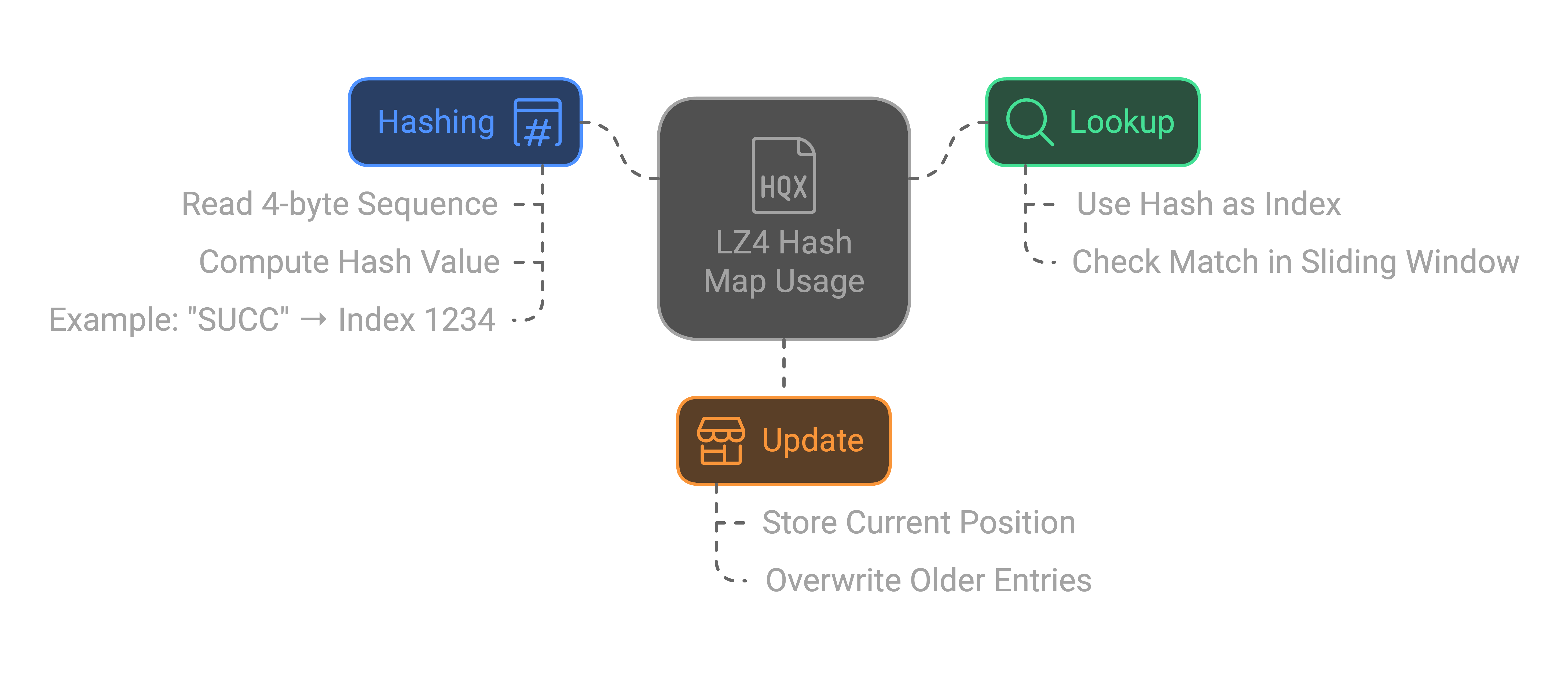
Take a 4-Byte Sequence: At each position in the input, read 4 bytes.
Hash the Sequence: Apply a lightweight hash function to the 4-byte sequence.
Example hash function:
hash = ((byte1 << 16) + (byte2 << 8) + byte3) * MAGIC_NUMBER >> (32 - HASH_BITS)
MAGIC_NUMBER and HASH_BITS are constants that determine the hash table size and distribution.
Store the Position: Store the current position of the sequence in the hash table at the computed hash index. If a collision occurs (i.e., the hash value already exists), overwrite the old position.
Advance to the Next Position: Slide one byte forward and repeat the process. The hash table only tracks positions within the sliding window. When the window slides, old entries in the hash table are overwritten.
Example walkthrough of compression
SUCCESS SUCCESS FAIL PENDING SUCCESS
Compressed Output
| Step | Current Sequence | Hash Value | Match Found? | Action | Token | Output Buffer (Stored on Disk) |
|---|---|---|---|---|---|---|
| 1 | SUCCESS | 1234 | No | Emit Literal | 0x70 | 0x70SUCCESS |
| 2 | SUCCESS | 1234 | Yes (Offset=0, Length=7) | Emit Match | 0x07 | 0x70SUCCESS0x07 |
| 3 | FAIL | 5678 | No | Emit Literal | 0x40 | 0x70SUCCESS0x070x40FAIL |
| 4 | PENDING | 9102 | No | Emit Literal | 0x70 | 0x70SUCCESS0x070x40FAIL0x70PENDING |
| 5 | SUCCESS | 1234 | Yes (Offset=8, Length=7) | Emit Match | 0x07 | 0x70SUCCESS0x070x40FAIL0x70PENDING0x07 |
so the final data which will be stored on disk would be SUCCESS SUCCESS FAIL PENDING SUCCESS --> 0x70SUCCESS0x070x40FAIL0x70PENDING0x07
- How many bytes did we save?
Uncompressed
8 (SUCCESS) + 8 (SUCCESS) + 5 (FAIL) + 8 (PENDING) + 8 (SUCCESS) = 37 bytes
Compressed
Tokens (5 bytes) + Literals (19 bytes) + Matches (4 bytes) = 28 bytes
we saved 9 bytes for this data not much huh? That's ~25% reduction, Let's say we have one column "Status" in which we are getting this data, in real world we will get thousands of rows. how much we will save in real world use case for similar data?
| Dataset Size | Original Size (GB) | Compressed Size (GB) | Bytes Saved (GB) | Compression Ratio |
|---|---|---|---|---|
| 1 Million Rows | 36 MB | 27 MB | 9 MB | 0.75 |
| 100 Million Rows | 3.6 GB | 2.7 GB | 0.9 GB | 0.75 |
| 1 Billion Rows | 36 GB | 27 GB | 9 GB | 0.75 |
All these savings with high speed (Compression and decompression speeds of 400-500 MB/s per core)
Example walkthrough of decompression
Let's take same data to decompress
Initialize Output BufferStart with an empty output buffer. This buffer will act as the reconstructed sliding window (dictionary).Process Each TokenEach token encodes: Literal Length: Number of bytes to copy directly to the output. Match Length: Number of bytes to copy from the already decompressed data.Copy LiteralsRead the literal length from the token. Copy that many bytes directly from the compressed stream to the output buffer.Reconstruct MatchesRead the match’s offset and length. Use the offset to find the start of the matching sequence in the output buffer. Copy the matching sequence into the output buffer for the specified length.Repeat Until DoneContinue processing tokens, literals, and matches until the compressed stream is fully expanded.
| Step | Token | Action | Match Details | Literal Data | Output Buffer |
|---|---|---|---|---|---|
| 1 | 0x70 | Copy Literal | N/A | SUCCESS | SUCCESS |
| 2 | 0x07 | Copy Match | Offset = 0, Length = 7 | N/A | SUCCESS SUCCESS |
| 3 | 0x40 | Copy Literal | N/A | FAIL | SUCCESS SUCCESS FAIL |
| 4 | 0x70 | Copy Literal | N/A | PENDING | SUCCESS SUCCESS FAIL PENDING |
| 5 | 0x07 | Copy Match | Offset = 8, Length = 7 | N/A | SUCCESS SUCCESS FAIL PENDING SUCCESS |
Best-Suited Data Types for LZ4
- Low-Cardinality Categorical Data
- Status codes: SUCCESS, FAIL, PENDING.
- Country codes: IN, US, UK.
- Boolean values: true, false.
Why: Repeated patterns compress exceptionally well with LZ4. Columns with few unique values result in high match ratios.
- Strings with Repeating Prefixes or Suffixes
- URLs: https://example.com/user/123, https://example.com/user/456.
- File paths: /var/logs/app1.log, /var/logs/app2.log.
Why: LZ4 identifies repeating patterns in prefixes/suffixes (e.g., https://example.com/) and encodes them efficiently using offsets.
- Numeric Data with Repeated or Incremental Values
- Timestamps: 1681234560, 1681234561, 1681234562.
- IDs: 1001, 1002, 1003.
Why:Incremental or repeated patterns can be encoded efficiently. Numeric columns often have localized patterns, especially when sorted.
- Sparse Data (Mostly Nulls or Defaults)
- Nullable columns: NULL, NULL, NULL, VALUE.
- Defaults: 0, 0, 0, 1.
Why: LZ4 can compact consecutive NULL or default values into small tokens.
Data Types Less Suitable for LZ4
- High-Cardinality Data
- Random strings: UUIDs (1a2b3c4d).
- Cryptographic hashes.
Why: High-cardinality data lacks repeating patterns, reducing compression opportunities.
Alternative: Consider algorithms like Zstandard for better compression ratios on high-entropy data.
- Already Compressed or Encrypted Data
- Gzip files, JPEG images, encrypted blobs.
Why: Compressed/encrypted data has high entropy and no visible patterns for LZ4 to exploit.
- Random or Unordered Numeric Data
- Random integers: 123, 9876, 5432.
- Unsorted timestamps.
Why: Lack of localized patterns makes pattern matching inefficient.
Optimization Tip: Sort the data to increase locality and improve match opportunities.
Optimization Tips for Using LZ4 in Columnar Databases
- Sort Columns Sorting data by frequently queried columns (e.g., timestamps) can significantly improve compression ratios.
Why:Sorting creates localized patterns, increasing the likelihood of matches. - Use Low-Cardinality Encodings For categorical data, use dictionary encoding before applying LZ4.
Example: Original: SUCCESS, FAIL, PENDING, SUCCESS. Encoded: 0, 1, 2, 0 (mapped to a dictionary like {0: SUCCESS, 1: FAIL, 2: PENDING}). Compressing encoded data yields better results.
Partition Data Strategically Partitioning by date, region, or other attributes helps localize patterns within partitions. Smaller partitions improve compression effectiveness.
Combine with Other Compression Techniques Hybrid Compression: Apply lightweight compression (e.g., Run-Length Encoding) to preprocess data before using LZ4.
Conclusion
While LZ4 isn't the best choice for high-entropy data, it remains an excellent tool for scenarios requiring fast decompression with moderate compression ratios. By understanding the data patterns and preprocessing strategies, you can maximize the benefits of LZ4 in your columnar database.